ゲームのバグって面白いですよね。進行不可能バグはもちろん論外ですが、ちょっとした不思議なバグはなかなかに楽しめます。
さて、今回話題になったのはWii版(バーチャルコンソール)のマリオ64で、「長時間たつと足場がどんどん浮き上がる」というものです。オリジナル版では起こらず、バーチャルコンソール版だけで起こるというのがミソです。
この摩訶不思議なバグがいったいどうやって起きているのか、確かめていきましょう。
話題のバグ:時間が経つと足場が浮かぶ
Automatonなどで記事になった「『スーパーマリオ64』を研究するプレイヤーたちは、Aボタンを押さずステージクリアするために3日間待ち続ける」がゲーマーの間で話題になっています。
このバグは、炎の海から顔を出したり沈んだりするだけの足場が、時間が経つにつれほんの少しずつ炎の海から浮遊するというものです。ゲームを起動したまま3日間放置すると、足場が十分な高さまで浮かび上がり、Aボタンを押さずとも次の足場まで進めることができます。
このバグの不思議なところは、オリジナルの64版では発生せず、Wiiへの移植で発生したというものです。「エミュのバグ」と一言で片付けてしまえばそれまでなのですが、実際どんなバグなのか、少しずつ紐解いてみましょう。
コンピュータと浮動小数点と精度
この現象を理解するには、まずコンピュータ(ゲーム機)がどのようにして数値を扱っているかということを理解しなくてはなりません。
現代のコンピュータは「0」と「1」の羅列、つまり2進数ですべての事象を扱います。このときの桁数のことをビット(bit)といいます。例えば「01」は2桁なので2bitですし、「01001」は5桁なので5bitです。
各ビットは2の累乗を表し、一番右の桁は2の0乗、つまり「1」を表します。一番右から2桁目は2の1乗なので「2」、右から3番目は2の2乗で「4」、という具合になります。あとは1になっているビットを足し合わせるだけで整数が作れます。
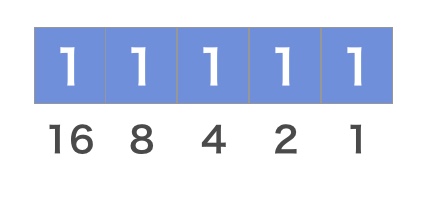
たとえば2進数の「101」は、「2の0乗(=1)」と「2の2乗(=4)」を足す(2の1乗のビットは「0」になっているので無視!)ので「5」になります。コンピュータではこんな風にして数値を表しています。
なお、マイナスを表したいときは一番左にビットを増やして、そのビットを数値ではなく「プラスかマイナスか」を表すビットとして扱うと表現できます。
浮動小数点
さて、2進数を使うことで任意の整数を表すことができました。次は小数です。
小数も、整数と同じく2進数で表現しないといけません。小数を扱う時は、2の0乗の右に2のマイナス1乗(つまり1/2)、その右に2のマイナス2乗(つまり1/4)と、どんどんマイナス乗の桁を増やしていきます。
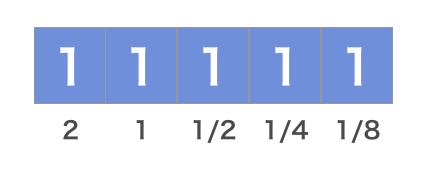
本当はもう少し複雑なのですが、ここでは割愛します。
この小数の表現方法を浮動小数点数、あるいは単に浮動小数点と呼びます。
浮動小数点の精度
実は浮動小数点にはひとつ問題があり、2の累乗と小数の噛み合わせが悪く、1/2 + 1/4 + 1/8 + 1/16 + ……では表しきれないことがかなりあります。例えば10進数の「0.1」は2進数ではうまく表せません。
2の累乗とうまく噛み合わない小数が出てくると、例えば正確に表すのに1万bit必要、とか、最悪の場合、2の累乗を足していっても表現しきれない場合は、桁数が「無限bit」必要になります。しかし当然1万bitや無限bit使うことは不可能です。なので現実ではある程度の精度で妥協しています。
浮動小数点は一般には32bitと64bitの形式が使われます。たとえ1万bit必要な小数でも32bitや64bitに押し込めます。このとき、どうしても誤差が発生してしまいます。もちろんbit数(桁数)が多いほど小数を細かく表すことができるので、精度が上がります。
ただし64bitでもせいぜい10進数での15桁程度の精度しかなく、32bitになると7桁程度の精度しかありません。小数を完全に表すのはほぼ不可能と思っていた方がいいです。
ここまでのまとめ
- コンピュータ(ゲーム機)は数値を0と1の2進数で表す
- 小数も2進数で表す
- 2の累乗を足し合わせてもうまく表現できない小数が存在する
- うまく表現できなくても32bitか64bitでむりやり近い値を表現する
- 小数を正確に表すのには64bitでも全然足りない
問題のプログラム
前提知識の説明は終わりました。ようやく本題に入れますね!
Googleドキュメントに上がっている解説を読むと、浮き沈みする足場は以下のようなプログラムで動いているそうです:
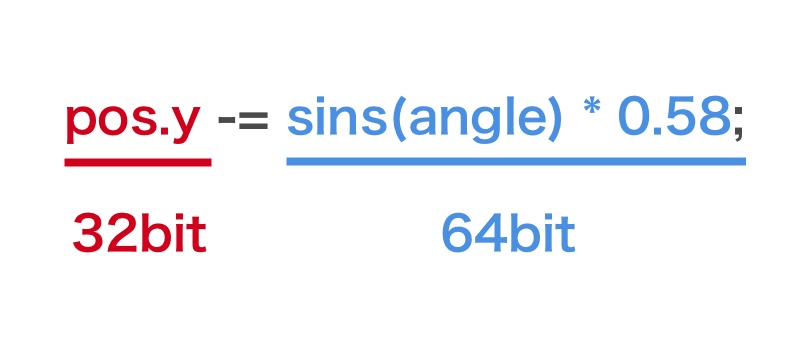
pos.y -= sins(angle) * 0.58;
angle += 0x100;1行目も2行目も、左辺がパラメータ(変化する値)で、右辺がパラメータにセットする値です。pos.yは足場のy座標でしょう。
このプログラムを読むと、三角関数のsin関数を使って足場の上下運動を実現しているようですね。sin関数は学校で習った通り、上下に揺れる波ですので、こいつに揺れ幅をかけてやれば後は勝手に揺れてくれます。今回は0.58の幅で揺れさせているようですね。そしてangleを少しずつ動かしてsin関数を動かすことにより、y軸に波を反映させています。
さて、ここで問題はpos.y(y軸)の値が実は32bitであるということと、右辺が64bitであるということです。32bitで0.58を表現するときは「0.58」ではなく「0.58f」と書かなければいけません。しかし今回は「f」がついておらず、64bitになっています。
計算に64bitが混ざると結果も64bitになるので、右辺全体は64bitです。そして左辺(pos.y)は32bitです。もちろん32bitの中に64bitは入りきらないので、強制的に32bitにされます。
トリックはここにあります。先述の通り、小数を表そうとすると64bitでも全然精度が足りないので、単純に32bitに落とすとぐちゃぐちゃになります。なので、なんらかのうまい手段で32bitに変換してやる必要があります。
そして、この64bitから32bitへ変換する手段が、64とWiiのVCとで、全く異なっているのです。64では最近接丸め(四捨五入のようなイメージ)で32bitへの変換が行われており、WiiのVCではゼロ方向への丸め(小数切り捨てのようなイメージ)で変換しています。
このとき、ゼロ方向への丸めは、どんどん原点(ゼロ)方向へと近づいていってしまう作用があります。これは普通の小数切り捨てで考えるとわかりやすいでしょう。「2.6」を小数切り捨てすると「2.0」になりますが、このとき-0.6だけ原点方向に動いています。マイナスの場合も考えて、「-2.6」を小数切り捨てすると「-2.0」となり、これもまた0.6だけ原点方向へ動いています。

このゼロ方向への丸めが諸悪の根源です。実際は小数7桁とかで丸めるので、誤差はごくごくわずかですが、この「原点方向への誤差」がどんどん積み重なって、ほんのちょっぴりずつ足場の位置がズレていきます。原点方向への誤差なので、位置はもちろん原点へと向かいます。
どこが原点になるかはゲームやステージによって違うのですが、「ほのおのうみのクッパ」ではステージの中心が原点となるようです。そして中心より高いところにある足場はどんどん下がっていき、中心より低い場所にある足場はどんどん上がっていきます。
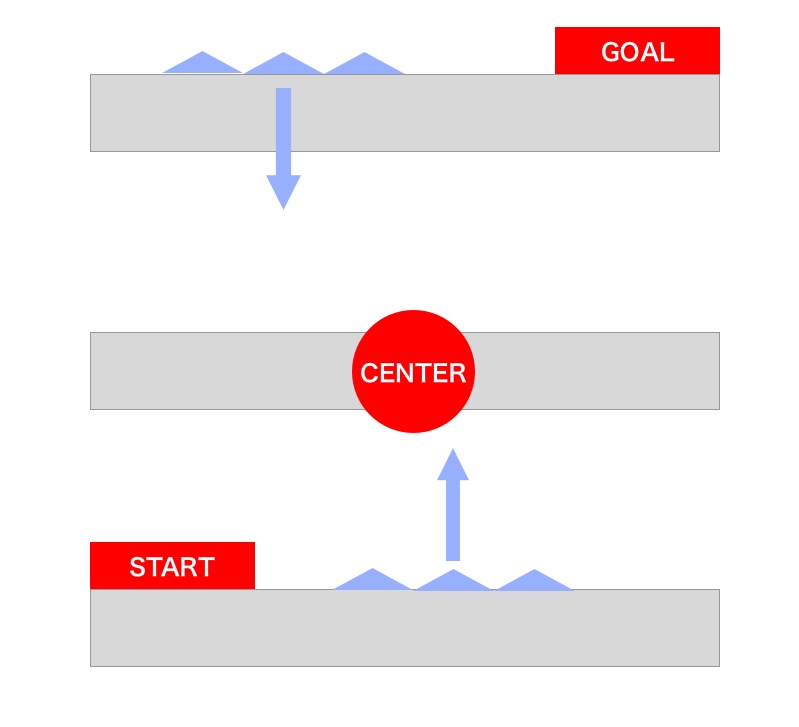
その結果として、スタート地点に近い足場は、どんどん浮上していくみたいです。
そもそもなぜ変換方法が食い違ったのか
そもそも移植なのにどうして食い違いが発生したのでしょう。実は64とWiiでは使っているCPUが違い、64は「MIPS」というCPUを使っており、Wiiは「PowerPC」というCPUを使っています。そして、Wiiに移植するときに、64bitから32bitに丸める命令を、挙動が違うものを選んでしまったようです。
ちなみに
「ファイアバブルランド」にも同様の足場がありますが、こちらは初めからy座標がゼロのところにいるので、この問題は発生しないようです。多層構造になっている「ほのおのうみのクッパ」ならではのバグですね。
