WebGL2入門 基礎編とWebGL2入門 最適化編では2D描画について扱いました。今回は3D表示に必要な知識について扱います。
WebGL2入門 記事一覧
前提となる知識
座標ベクトルについて
WebGL2では座標ベクトル(x, y, z, w)は列ベクトルになります。プログラムが横書きなので横に並べて書いているだけです。よって数学の教科書に書いてある座標変換と同じように考えることができます。
同次座標(Homogeneous Coordinate)
WebGL2では座標は(x, y, z, w)の4要素のベクトルです。これは、後述する平行移動を実現するために、どうしてもwが必要になるからです。ではwは単なる計算上のダミーかというと、そういうわけではありません。WebGL2では最終的にxyzの値をそれぞれwで割ることにしています。つまり(x, y, z, w)は(x/w, y/w, z/w)ということになります。この座標の表現方法は同次座標と呼ばれています。
同次座標は、w=1のときは普通のベクトルとみなすことができます。1で割っても値は変わりません。ですが、w≠1のときは値が変わってしまいます。このときのwは、主に遠近感を表すのに使用されます。遠くの頂点に大きなwを設定することで、「遠くのものほど小さく見える」を実現することができます。
行優先(Row-major)と列優先(Column-major)
プログラミング上の問題として、行列をどういったデータ構造で表すか、というのがあります。
行列は主に1次元配列で表すのですが、そのとき、1行目、2行目…と行ごとにデータを並べるのか、あるいは、1列目、2列目…と列ごとにデータを並べていくのかということが問題になります。このとき行ごとにデータを並べていく方式を行優先、列ごとに並べていく方式を列優先といいます。
たとえば以下のような行列があるとします。

このとき行優先だと[1, 2, 3, 4, 5, 6, 7, 8, 9]、列優先だと[1, 4, 7, 2, 5, 8, 3, 6, 9]となります。
WebGL2ではデフォルトの設定では列優先を用います。
3D描画のための座標変換
3Dグラフィックスを画面に表示するには、ちょっとした決まりごとがあります。どのようなデータを用意してどう使うかは自由ですが、最終的には一定のルールに従ったデータ形式に変換する必要があります。
正規化デバイス座標(Normalized Device Coordinates, NDC)
WebGL2では、最終的に座標を正規化デバイス座標におさめる必要があります。正規化デバイス座標はそれぞれの軸が-1.0から1.0までの値をとる座標で、立方体の形をしています。また、正規化デバイス座標では左手座標系(Z軸の奥がプラス)を採用しています。
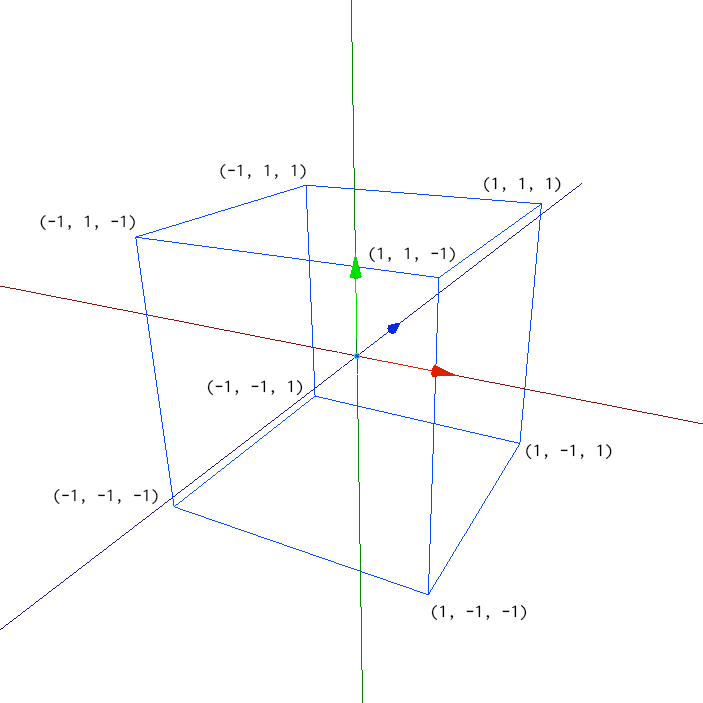
正規化デバイス座標(NDC)
これがWebGL2におけるたったひとつの決まりごとです。何をしても、最終的にこの正規化デバイス座標へと収まっていればいいのです。しかし正規化デバイス座標をそのまま扱うのは非常に困難です。よって通常は用意した座標にいくつかの変換行列を掛け合わせて、正規化デバイス座標に落とし込むことになります。
WebGL2の座標系
今までの記事では「WebGL2は右手座標系」と言ってきましたが、ここでは最終出力である正規化デバイス座標は左手座標系を採用しています。なぜわざわざ正反対の座標系を採用しているのでしょうか。
これに対する回答としては「そういう慣習だから」と答えるほかありません。参考書やライブラリの多くが右手座標系を採用しているので、それに従っておくのがいいでしょう。ただ、左右両方に対応しているものや、左手座標系を採用しているライブラリも中にはあるので、そのときどきに合わせたものを採用しましょう。
モデル変換行列
3Dオブジェクトはそれぞれ自分中心のオブジェクト座標を持っています。モデリングソフトなどでも、3Dモデルはオブジェクト座標を中心に作成します。
モデルはオブジェクト座標に配置される
これはモデルがひとつだけなら何の問題も起こりません。では、モデルが複数あった場合はどうでしょうか。オブジェクト座標は自分自身のことしか考えておらず、モデルが複数になると重りあったりしてしまい、すぐに破綻します。したがってモデルを配置するときはそれぞれのオブジェクト座標を自分自身の座標ではなく「世界から見た客観的な座標」に配置する必要があります。この世界の座標のことをワールド座標と言い、配置の変換を行う行列をモデル変換行列と言います。
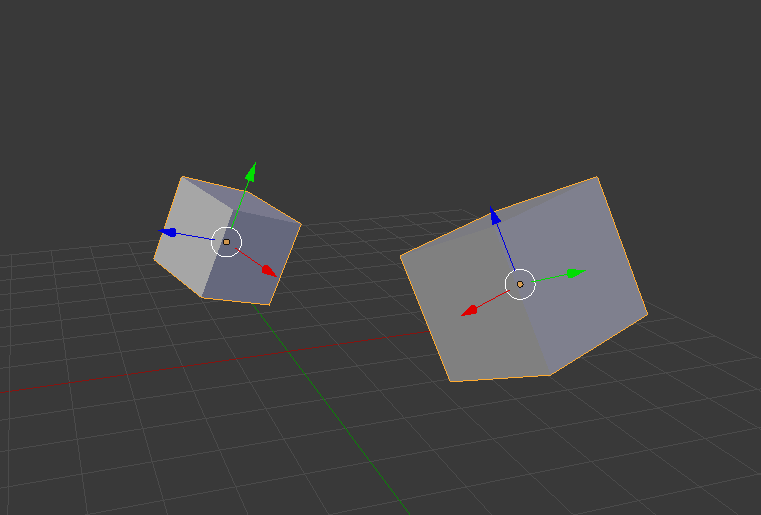
それぞれのモデルをワールド座標に配置する
モデル変換行列は主に平行移動、拡大縮小、回転の3つから構成されます。
平行移動(Translation)
平行移動量をそれぞれTx、Ty、Tzとすると、平行移動行列は以下のようになります。
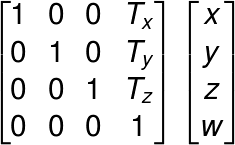
これで平行移動になることが理解できなければ実際に手で計算してみてください。
拡大縮小(Scale)
xyzをそれぞれSx, Sy, Sz倍するだけなので行列は以下のようになります。
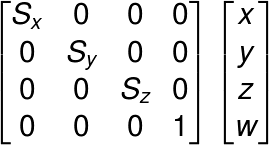
回転(Rotation)
これは少し複雑です。まずはz軸まわりの回転について考えましょう。
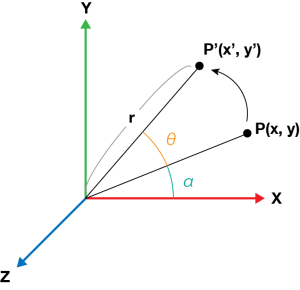
点Pをθラジアンだけ回転させ、点P’へうつす変換を考えます。原点から点Pまでの距離をr、X軸と点Pがなす角をαとします。このとき点Pは(x, y) = (rcosθ, rsinθ)で表せます。同様に点P’は(x’, y’) = (rcos(α+θ), rsin(α+θ))と表せます。
ここで加法定理を用いてx’を展開すると、x’ = r(cosα・cosθ – sinα・sinθ) = rcosα・cosθ – rsinα・sinθ = xcosθ – ysinθとなります。y’についても同様に、y’ = xcosθ + ysinθとなります。
よって点P’は、(x’, y’) = (xcosθ – ysinθ, xcosθ + ysinθ)となります。これを行列で表現すれば回転行列になります。また、他の軸についても同様に求めます。すると以下のようになります。
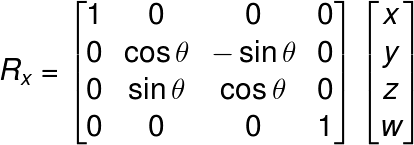
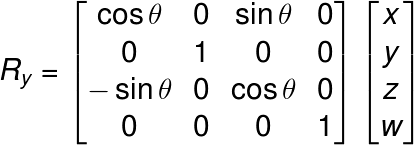
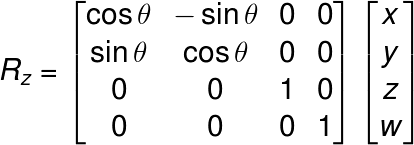
ビュー変換行列
モデルをワールド座標へ配置したら、次はカメラの位置と向きを決めます。カメラを決定する行列は、ビュー変換行列と言われています。
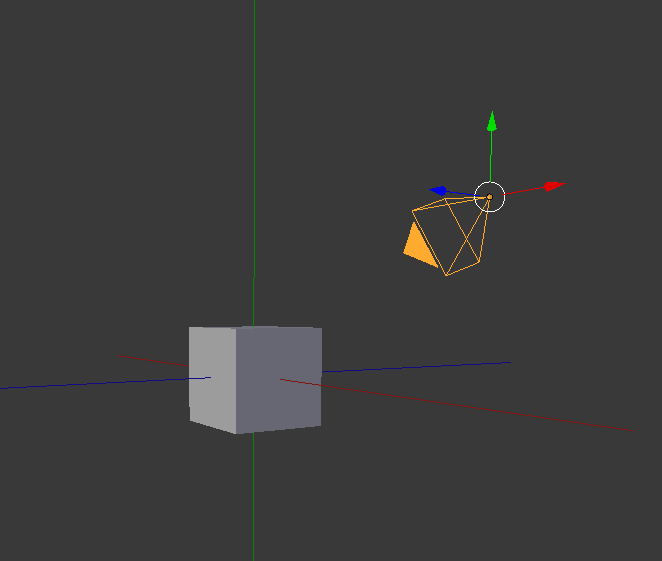
カメラを越しに見ているという設定

カメラの位置や角度によって、見え方は様々になる
ビュー変換行列は平行移動と回転だけで実現できます。もっとも単純な方法では、カメラ位置を原点に移動して、必要なだけ回転させれば、それだけで出来上がります。ですが、これだけでは「どこを向くか」の設定が難しく、実用性にかけます。そこで、この記事ではかわりにlook atという方式について説明します。
look atに必要なパラメータは、カメラの位置、カメラの見ている位置、カメラの上方向、の3つです。カメラの上方向というのは、たとえばカメラを普通に構えていれば(0, 1, 0)になりますし、横倒しに構えていたら(1, 0, 0)などになります。
カメラ位置をC = (Cx, Cy, Cz)、カメラの見ている位置をL = (Lx, Ly, Lz)、カメラの上方向をU = (Ux, Uy, Uz)とします。また、カメラから見た座標のことを、ここではカメラ座標とします(※一般にはそう呼びません)。パラメータが決まれば、あとは平行移動と回転だけで実現できます。
まずカメラ座標の原点をワールド座標の原点に持ってくるように平行移動します。これは単に(-Cx, -Cy, -Cz)の平行移動をするだけです。
次に回転行列です。まずはカメラ座標に関する情報が必要になるので、カメラ座標の基底ベクトルを求めます。L(見ている方向)が正面に来るようにするので、CとLを通る直線がZ軸になります。右手座標系ではZ軸のマイナス方向が奥だということを考慮すると、LからCへのベクトルを求め正規化すればZ軸が求まります。
まずカメラ座標のZ軸をZ’とすると、Z’ = (C-L)/|C-L|となります。X軸はZ’とUに対して垂直なので、外積を求めてから正規化すれば、X’=(U×Z’)/|U×Z’|となります。同様にY’=(Z’×X’)/|Z’×X’|。これで軸が求まりました。ここで求めた基底は、それぞれ直行しており、また正規化されているので、正規直交基底となります。
基底が求まったので、回転します。ワールド座標もカメラ座標も正規直交基底を持つので、回転行列を使わずとも、規定を変換してやるだけで求まります。今の所役目のないwは省略して、ワールド座標上の点を(x, y, z)、カメラ座標上の点を(x’, y’, z’)とすると、以下のような関係が成り立ちます。
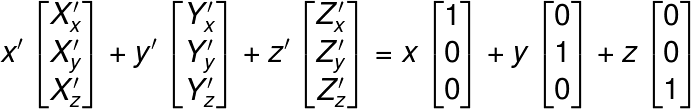
これを変換行列の形で書くと、
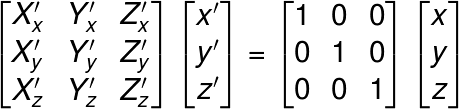
あとは左側から逆行列をかけてやって、
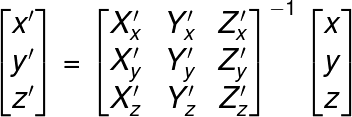
となります。これでカメラ座標が求まりました。あとはこの逆行列を求めるだけなのですが、カメラ座標の基底は正規直交基底なので、X’, Y’, Z’はそれぞれ直行していて長さが1です。よってそれぞれの内積を計算してやると、X’・X’=1、X’・Y’=0、X’・Z’=0、…のようになります。このことを考えると、転置するだけで逆行列が求まります。よくわからないという人は実際に転置した行列をかけてみてください。
さて、これで平行移動の行列と回転の行列が求まりました。このふたつをかけたものが求めるビュー変換行列となります。
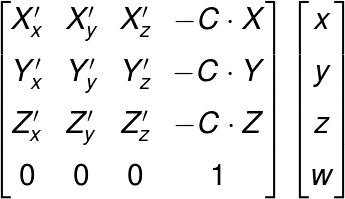
プロジェクション変換行列
プロジェクション変換行列は、どこまでのものが、どのように見えるかということを決定する行列です。わかりやすく言えば、視野を決める行列ということになります。変換後の座標はクリップ座標と呼ばれています。クリップ座標はプロジェクション変換によって得られる有限の空間で、座標の外にある物は描画されません。クリップ座標からは左手座標系になるので、右手座標系を使っている場合は、ここでZ座標の符号を反転しておきましょう。また、いわゆる「パースをつける」こともプロジェクション変換行列の仕事になります。遠くの物を小さく表示したいのなら、ここで縮小しておきましょう。
プロジェクション変換行列で用いられるのは主に2種類で、パースのつかない平行投影と、パースのついた透視投影です。

平行投影と透視投影
並行投影(Orthographic Projection)
平行投影は、近くの物も遠くの物も同じ大きさで表示します。また、視野の広がりも持たず、四角い窓を通して見たような表示結果になります。例えば、数学の授業で使う立体図形などは、平行投影と言えます。
必要なパラメータは、視野の上下左右(top, bottom, left, right)の座標と、前面および背面までの距離(near, far)になります。nearとfarには0や負の値を指定することも可能です。ここで定められる空間のことをビューボリューム(View Volume)と言います。
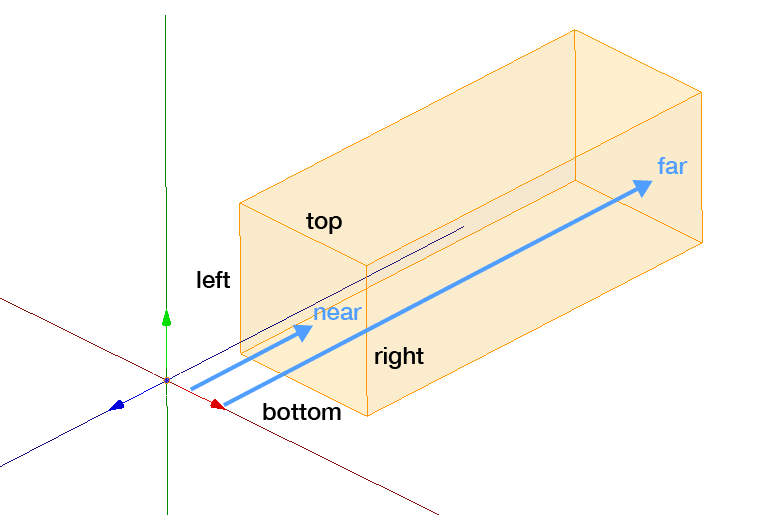
図を見れば明らかですが、平行投影の場合は、ビューボリュームは単なる直方体で、パースも考慮しなくてかまいません。つまり、平行投影の場合、クリップ座標と正規化デバイス座標は一致します。三次元である正規化デバイス座標と、四次元で表されるクリップ座標とは、厳密には違うのですが、平行投影ではwの値が常に1になり、何の影響も与えないので無視してかまいません。よって、クリップ座標のことは考えずに、正規化デバイス座標へ変換すると考えたほうが単純でいいでしょう。
正規化デバイス座標へ変換するには、この直方体をそのまま各軸について-1.0から1.0までの値を取るような長さ2の立方体に変換するだけでできます。具体的な変換手順は以下の通り。
- ビューボリュームの中心を原点へ移動する
- 各辺をそれぞれの長さで割って、長さ1の立方体にする
- 各辺を2倍に拡大して長さ2の立方体にする
- Z座標を反転して左手座標系に変換する
これを行列にまとめると以下のようになります。
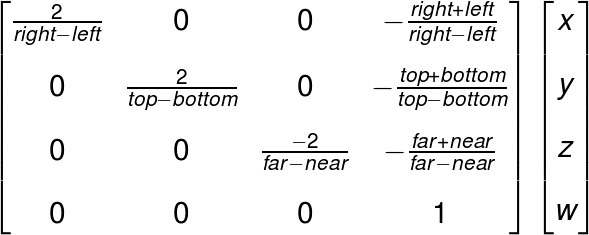
透視投影(Perspective Projection)
透視投影は、遠くの物ほど小さく見える、パースのついた表示になります。こちらを使うことの方が多いでしょう。必要なパラメータは平行投影と同じです。ただし、nearとfarには正の値を指定する必要があります。
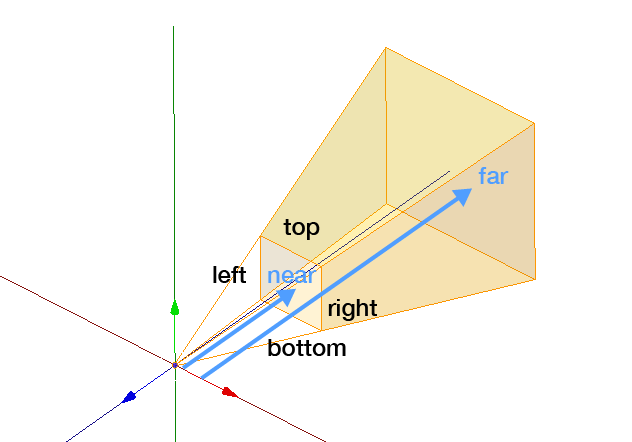
このビューボリュームは、視野錐台(View Frustum)とも呼ばれます。
透視投影によるクリップ座標への変換方法については、ここでは割愛します。変換行列は以下のようになります。
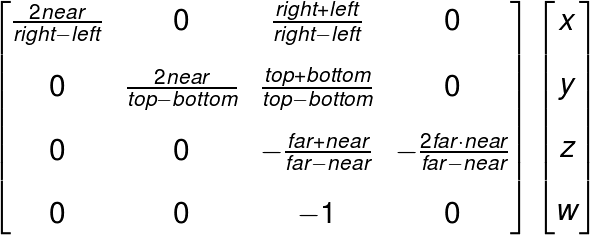
クリップ座標から正規化デバイス座標へ
最後にクリップ座標から正規化デバイス座標へ変換するために、xyzの値をそれぞれwで割って(x/w, y/w, z/w)とする必要がありますが、これはバーテックスシェーダが自動でやってくれるので、我々が明示的にやる必要はありません。
