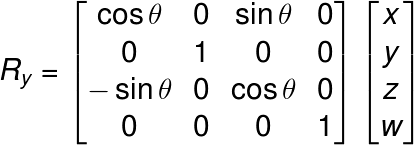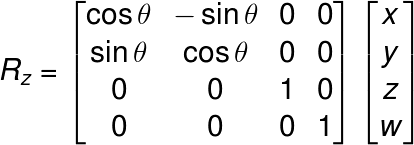前回の記事では簡単な2D表示について取り扱った。今回は3D表示について取り扱う。
3D表示とは言っても、2Dのときと大きく変わることはない。WebGLはそもそも3Dグラフィックス用のAPIなのだ。よってせいぜいシェーダを少し書き換えて、ちょっとした行列操作が加わる程度の違いになる。
DartでWebGL入門
前知識
座標ベクトルについて
WebGLでは、座標ベクトル(x, y, z, w)は列ベクトルだ。プログラムが横書きである以上、縦に並べることができないので、横書きにしているだけである。よって、数学の教科書に載っている座標変換行列の例と全く同じように考えればよい。
同次座標(Homogeneous Coordinate)
WebGLで使用する座標はxyzwの4次元ベクトルである。後述する平行移動を行列の積であらわそうとすると、どうしても1次元増やす必要があるのだ。ではwは単なるダミーなのかというと、必ずしもそうではない。WebGLでは最終的にxyzの値をwで割ることにしている。つまり(x, y, z, w)=(x/w, y/w, z/w)ということになる。この表現は同次座標(Homogeneous Coordinate)と呼ばれている。
同次座標は、w=1なら単なる3次元ベクトルと同じようにみなすことができる。w≠1のときについては、wの値は、主に遠近感を表現するのに使用される。遠くの頂点に大きなwを設定することで、「遠くの物ほど小さく見える」という現象を再現することができるのだ。
行優先(Row-major)と列優先(Column-major)
数学には存在しないプログラミング特有の問題として、行列を行優先・列優先のどちらで表現するのか、というものがある。プログラム上では、行列は2次元配列ではなく1次元の配列として表す。DartではFloat32Listを使用する。
行列を1次元配列に落とし込むとき、1行目、2行目、と行ごとに並べていくのか、あるいは1列目、2列目、と列ごとに並べていくかということが問題になる。このとき1行目、2行目…と並べていく方式を行優先、1列目、2列目…と並べていく方式を列優先と呼ぶ。
例えば以下のような行列Aを考える。
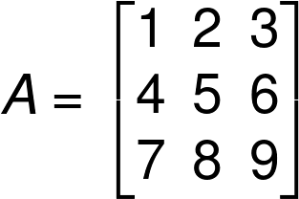
このとき、行優先ならば[1, 2, 3, 4, 5, 6, 7, 8, 9]になり、列優先だと[1, 4, 7, 2, 5, 8, 3, 6, 9]になる。
WebGLでは行列の表現に列優先を用いる。
3D描画のための座標変換
3Dグラフィックスを画面に表示するには、ちょっとした決まり事がある。どんなデータを用意してどう使うかはユーザの自由ではあるが、最終的には一定のルールに従ったデータに変換する必要がある。
正規化デバイス座標(Normalized Device Coordinates, NDC)
WebGLでは、座標を正規化デバイス座標と呼ばれる座標に収める必要がある。正規化デバイス座標はそれぞれの軸が-1.0から1.0までの値を取る座標だ。正規化デバイス座標は左手座標系(Z軸のプラス方向が奥)を採用している。
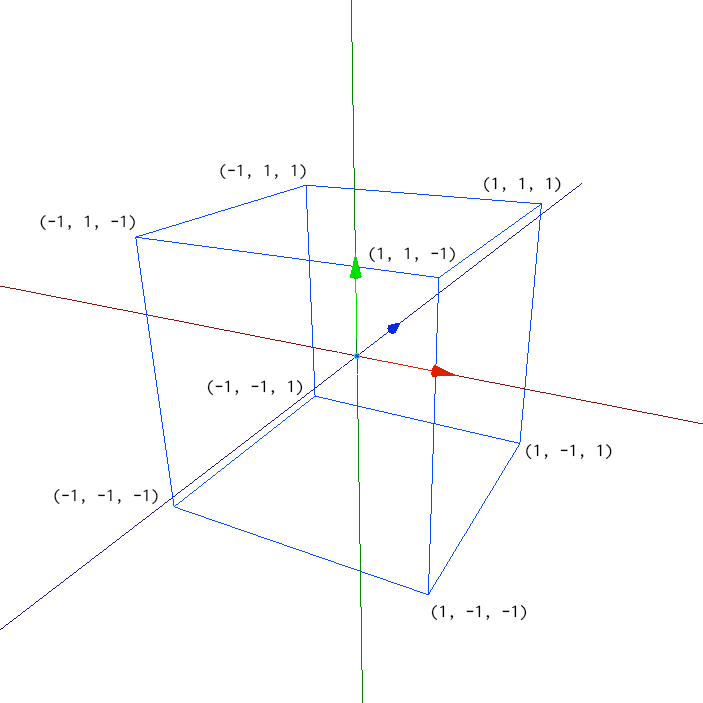
正規化デバイス座標(NDC)
これが、たったひとつの決まり事である。最終的に正規化デバイス座標にさえ収まっていれば、何をしてもかまわない。しかし現実問題として、正規化デバイス座標をそのまま扱うのは困難だ。よって、独自の扱いやすい座標に変換行列を掛け合わせて、正規化デバイス座標へ落とし込むのが一般的な手法になる。
WebGLの座標系
前回の記事で、WebGLでは主に右手座標系を用いると述べたが、最終出力である正規化デバイス座標とは逆の座標系を選択していることになる。わざわざZ軸を反転させなければならず、少し不自然だ。
これに対する理由としては「そういう慣習だから」と答えるほかない。参考書やライブラリの多くが右手座標系をデフォルトとしているので、従っておくのが楽でいいだろう。ただし、左右両方に対応しているライブラリや、左手座標系をデフォルトとするフレームワークも存在するので、そのときどきの環境に合わせた選択をしよう。
モデル変換行列
一般に、3Dモデルはそれぞれ自分中心のオブジェクト座標を持っている。モデリングソフトなどでも、3Dモデルはオブジェクト座標を基準に作成する。
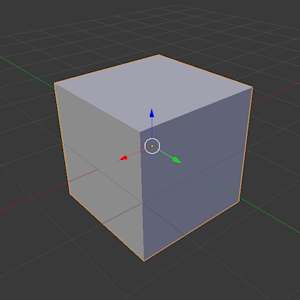
モデルはオブジェクト座標に配置される
モデルがひとつだけなら何も問題は起こらない。しかし複数のモデルを同じ空間に配置する場合はどうだろうか。オブジェクト座標は自分自身のことしか考慮しておらず、モデルが複数になると同じ場所に重なり合ってしまい、破綻する。よって複数のモデルを配置するときは、それぞれのモデルのオブジェクト座標を「世界」の空間、ワールド座標に配置する必要がある。これを実現する変換行列は、モデル変換行列と呼ばれている。
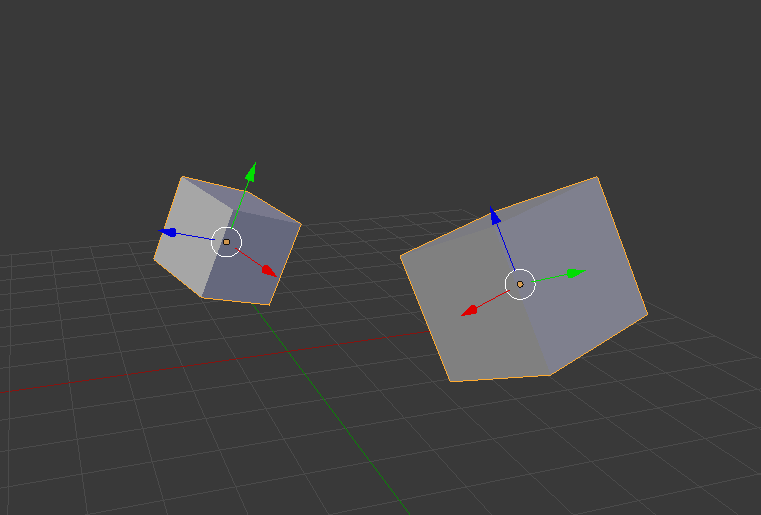
オブジェクト座標を持つそれぞれのモデルをワールド座標に配置する
モデル変換行列は主に平行移動、拡大縮小、回転の3つから構成されている。拡大縮小・回転でサイズや角度を決めて、平行移動でワールド空間座標へ配置するという手順が一般的だ。
平行移動(Translation)
3Dグラフィックスでは、平行移動も掛け算として表すのが一般的だ。平行移動量をそれぞれTx、Ty、Tzとしたときの平行移動行列は、
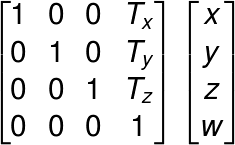
となる。妙なことをしていなければこの時点でのwの値は1になるので、これで本当に平行移動になるのか理解できないときは、手計算してみるといい。
プログラム上での表記は列優先になることには注意したい。以下にDartで記述した例を記しておく。
var translation = new Float32List.fromList([1.0, 0.0, 0.0, 0.0,
0.0, 1.0, 0.0, 0.0,
0.0, 0.0, 1.0, 0.0,
tx, ty, tz, 1.0]);拡大縮小(Scale)
拡大率をそれぞれSx, Sy, Szとしたときの 拡大縮小行列は、
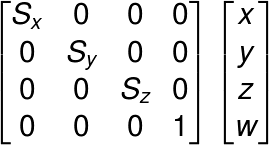
となる。x, y, zをそれぞれSx, Sy, Sz倍しているだけだ。
回転行列(Rotation)
これは少しややこしい。まずはZ軸周りの回転について考えてみよう。
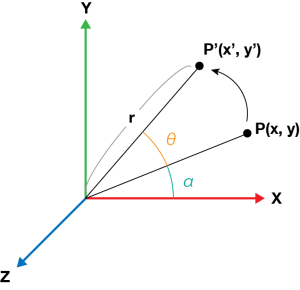
点Pを原点周りにθラジアン回転し、点P’へうつす変換を考える。原点から点Pまでの距離をr、X軸と点Pがなす角をαとすると、点Pは(x, y)=(rcosθ, rsinθ)と表すことができる。同様に点P’は(x’, y’)=(rcos(α+θ), rsin(α+θ))と表せる。
ここで加法定理を用いてx’を展開すると、x’ = r(cosα・cosθ-sinα・sinθ) = rcosα・cosθ – rsinα・sinθ = xcosθ – ysinθとなる。y’についても同様に、y’ = xcosθ + ysinθとなる。
よって点P’は、(x’, y’) = (xcosθ – ysinθ, xcosθ + ysinθ)。あとはこれを行列で表現してやればよい。他の軸についての回転も同様に求めることができる。
従って、回転角をθラジアンとしたとき、それぞれの軸について回転した座標ベクトルをRx、Ry、Rzとすると、回転行列は、
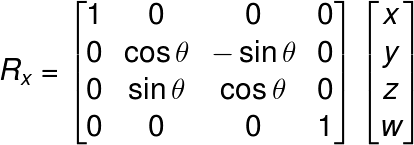
となる。Dartでは以下のようになる。
var rotationX = new Float32List.fromList(<double>[1.0, 0.0, 0.0, 0.0,
0.0, cos(radian), sin(radian), 0.0,
0.0, -sin(radian), cos(radian), 0.0,
0.0, 0.0, 0.0, 1.0]);
var rotationY = new Float32List.fromList(<double>[cos(radian), 0.0, -sin(radian), 0.0,
0.0, 1.0, 0.0, 0.0,
sin(radian), 0.0, cos(radian), 0.0,
0.0, 0.0, 0.0, 1.0]);
var rotationZ = new Float32List.fromList(<double>[cos(radian), sin(radian), 0.0, 0.0,
-sin(radian), cos(radian), 0.0, 0.0,
0.0, 0.0, 1.0, 0.0,
0.0, 0.0, 0.0, 1.0]);ビュー変換行列
各モデルをワールド座標へ配置し終えたら、次はカメラの位置と向きを決める。カメラの位置と向きを決定する変換行列は、ビュー変換行列と呼ばれている。
カメラを越しに見ているという設定

カメラの位置や角度によって、見え方は様々になる
ビュー変換行列は平行移動と回転だけで実現できる。最も単純な方法としては、カメラ位置を原点に平行移動して、必要なだけ回転させれば、それで終わりだ。しかし、これでは「どこを向くか」を指定するのが難しく、実用性に欠けるので、この記事では取り扱わない。代わりにlook atと呼ばれる方式について説明する。
必要なパラメータはカメラの位置、カメラの見ている位置、カメラの上方向、の3つになる。カメラの上方向というのは、例えば普通にカメラを構えていれば(0, 1, 0)になるし、横倒しになっていたら(1, 0, 0)などになる。
カメラ位置をC=(Cx, Cy, Cz)、見ている位置をL=(Lx, Ly, Lz)、上方向をU=(Ux, Uy, Uz)としよう。また、カメラから見た座標のことを、ここではカメラ座標と呼ぶことにする(※あまり一般的な呼び方ではない)。パラメータを決定したら、あとは平行移動と回転をするだけだ。
まずはカメラ座標の原点(カメラの位置)をワールド座標の原点へ持ってくるように平行移動する。単に(-Cx, -Cy, -Cz)だけ平行移動すればいい。
次に回転行列について考える。はじめに、カメラ座標についての情報が必要なので、カメラ座標の基底ベクトルを求める。Lが正面に来るようにするのだから、CとLを通る直線がZ軸になる。右手座標系ではZ軸のマイナス方向が奥だということを考慮すると、LからCへのベクトルを求め正規化すればZ軸が求まる。よってカメラのZ軸をZ’とすると、Z’=(C-L)/|C-L|となる。X軸はZとUに垂直なので、外積を求めてから正規化する。よってX’=(U×Z)/|U×Z|。同様にして、Y’=(Z×X)/|Z×X|=Z×X。ここでY≠Uであることに注意したい。たとえばカメラが少し斜め上を向いているとすると、実際のY軸は少し傾くので、Uと一致しない。Uはせいぜい「Z軸から見てどちら側が上か」を表す程度になる。ここで求めたカメラ座標の基底は、それぞれ直交しており、長さも正規化されているので、正規直交基底となる。
あとはカメラ座標の軸をワールド座標の軸と一致するように回転するだけだ。回転行列を使って回転してもいいだろうが、ワールド座標もカメラ座標も、どちらも正規直交基底なので、基底を変換してやる方が早いだろう。今のところ役目のないwは一旦省略して、ワールド座標上の点を(x, y, z)、求めるカメラ座標上の点を(x’, y’, z’)で表すと、2つの座標の間に以下の関係が成り立つ。
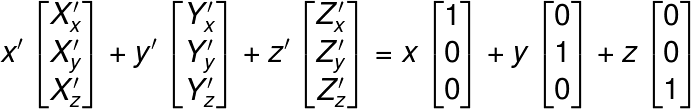
これを変換行列の形で表記すると、
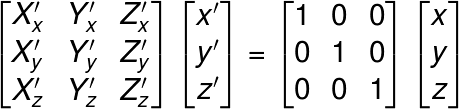
となる。次に左側から逆行列をかけて、
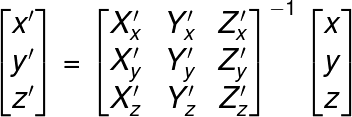
と変形できる。これでカメラ座標上の点(x’, y’, z’)が求まった。さて、あとはこの逆行列なのだが、カメラ座標の基底は正規直交基底なので、X、Y、Zはそれぞれ直交していて、かつ長さが1だ。それぞれ内積を計算すると、X’・X’=1、X’・Y’=0、X’・Z’=0、…のようになる。なので、転置してやるだけで逆行列になる。よくわからないなら、実際に手計算で転置した行列を掛けてみるといいだろう。
これで平行移動と回転の行列が求まったので、2つを掛けたものが、求めるビュー変換行列となる。
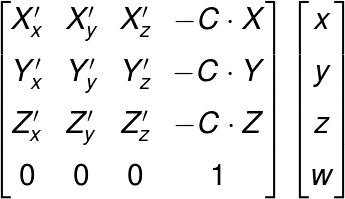
Dartでは以下のようになる。
var view = new Float32List.fromList(<double>[xx, yx, zx, 0.0,
xy, yy, zy, 0.0,
xz, yz, zz, 0.0,
-cx, -cy, -cz, 1.0]);プロジェクション変換行列
プロジェクション変換行列は、どこまでのものが、どのように見えるかを決定する。わかりやすく言えば、視野を決めるということになる。変換後の座標は、クリップ座標と呼ばれている。クリップ座標はプロジェクション変換によって得られる有限の空間で、座標の外にある物は描画されない。クリップ座標からは左手座標系になるので、右手座標系を使っている場合は、ここでZ座標の符号を反転しておく。また、いわゆる「パースをつける」こともプロジェクション変換行列の仕事になる。遠くの物を小さく表示したいのなら、ここで縮小しておこう。
プロジェクション変換行列で用いられるのは主に2種類で、パースのつかない平行投影と、パースのついた透視投影だ。

平行投影と透視投影
平行投影(Orthogonal Projection)
平行投影は、近くの物も遠くの物も同じ大きさで表示する。また、視野の広がりも持たず、四角い窓を通して見たような表示結果になる。例えば、数学の授業で使う立体図形などは、平行投影だ。
必要なパラメータは、視野の上下左右(top, bottom, left, right)の座標と、前面および背面までの距離(near, far)になる。nearとfarには0や負の値を指定することも可能だ。ここで定められる空間のことをビューボリューム(View Volume)という。
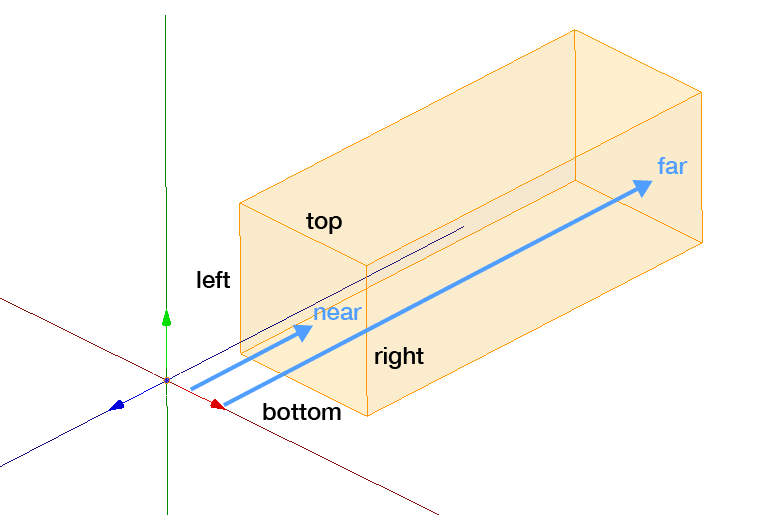
平行投影のビューボリューム
図を見ればわかると思うが、平行投影の場合は、ビューボリュームは単なる直方体で、パースも考慮しなくていい。つまり、平行投影の場合、クリップ座標と正規化デバイス座標は一致する。三次元である正規化デバイス座標と、四次元で表されるクリップ座標とは、厳密には違うのだが、平行投影ではwの値が常に1になり、何の影響も与えないので無視してよい。よって、クリップ座標のことは考えずに、正規化デバイス座標へ変換すると考えたほうが単純でいいだろう。
正規化デバイス座標へ変換するには、この直方体をそのまま各軸について-1.0から1.0までの値を取るような長さ2の立方体に変換するだけでいい。具体的な変換手順は以下の通りだ。
- ビューボリュームの中心を原点へ移動する
- 各辺をそれぞれの長さで割って、長さ1の立方体にする
- 各辺を2倍に拡大して長さ2の立方体にする
- Z座標を反転して左手座標系に変換する
これを行列にまとめると、
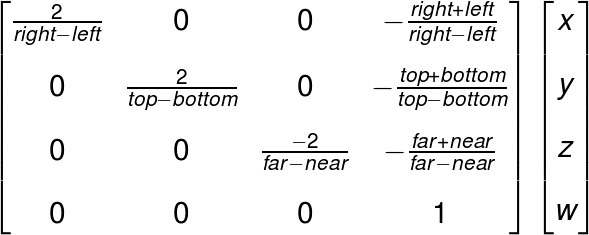
となる。この行列を列優先で表記すると以下のようになる。
var ortho = new Float32List.fromList(<double>[2/(right-left), 0.0, 0.0, 0.0,
0.0, 2/(top-bottom), 0.0, 0.0,
0.0, 0.0, -2/(far-near), 0.0,
-(right+left)/(right-left), -(top+bottom)/(top-bottom), -(far+near)/(far-near), 1.0]);
透視投影(Perspective Projection)
透視投影は、遠くの物ほど小さく見える、パースのついた表示になる。こちらを使うことの方が多いだろう。必要なパラメータは平行投影と同じだ。ただし、nearとfarには正の値を指定する必要がある。
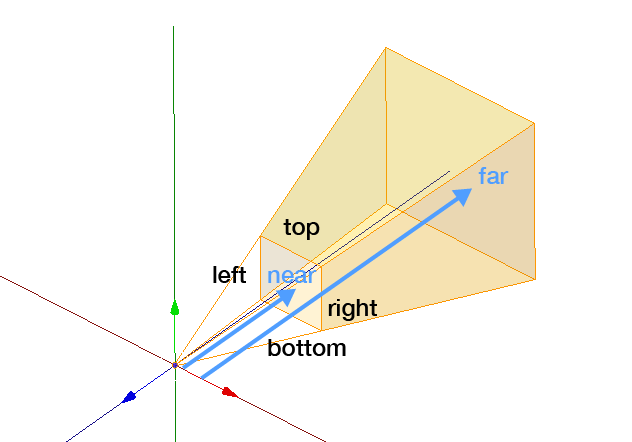
透視投影のビューボリューム
このビューボリュームは、視野錐台(View Frustum)とも呼ばれる。
透視投影によるクリップ座標への変換方法については、別記事で解説予定なので、ここでは割愛する。変換行列は以下のようになる。
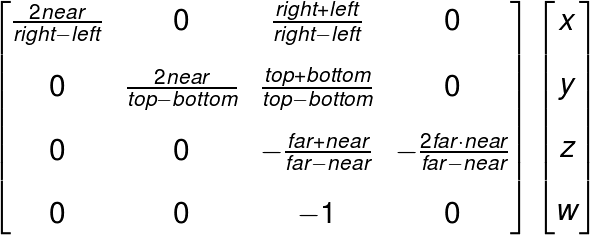
列優先で表記すると以下のようになる。
var proj = new Float32List.fromList(<double>[(2*near)/(right-left), 0.0, 0.0, 0.0,
0.0, (2*near)/(top-bottom), 0.0, 0.0,
(right+left)/(right-left), (top+bottom)/(top-bottom), -(far+near)/(far-near), -1.0,
0.0, 0.0, -(2*far*near)/(far-near), 0.0]);クリップ座標から正規化デバイス座標へ
クリップ座標のxyzの値をそれぞれwの値で割れば正規化デバイス座標(x/w, y/w, z/w)が得られる。この作業はバーテックスシェーダの仕事なので、ユーザがやる必要はない。
3D描画のための設定(一部)
WebGLには細かい描画設定があるので、その中からよく使うものを紹介したい。
ワインディングオーダー(Winding Order)
前回の記事で、WebGLでは反時計回り(Counter Clockwise)に頂点を配置するとポリゴンが表に……と書いたが、反時計回りは単にデフォルト値であるだけで、実際には変更できる。この順序のことをワインディングオーダーと呼ぶ。ここでは変更はしないが、必要ならば設定しておこう。
context.frontFace(CW); // 時計回り
context.frontFace(CCW); // 反時計回り背面カリング(Backface Culling)
負担を軽減するために描画に不要なポリゴンを省くことをカリングという。背面カリングはもっとも単純なカリング方法で、裏を向いているポリゴンを描画しないようにする。逆に言えば、背面カリングを有効にしないかぎり、ポリゴンの裏側も描画される。3Dグラフィックスを扱うならば有効にしておこう。背面カリングは、enableメソッドを使用することで有効化できる。
context.enable(CULL_FACE);無効化するには、disableメソッドを使用する。
context.disable(CULL_FACE);デプステスト(Depth Test)
デプステスト、あるいは深度テストというのは、その名の通り描画対象の深度を調べる工程だ。デフォルトでは奥行きを無視して後に描画したオブジェクトほど上に表示されるが、通常は手前のオブジェクトが奥のオブジェクトを隠すように描画したいだろう。デプステストを使えばこれを実現することができる。
WebGLではデプスバッファと呼ばれるバッファが用意されており、ピクセルごとに現在の深度値がここに書き込まれる。デプステストを有効化していると、書き込もうとしているフラグメントの深度値とデプスバッファの深度値を比較し、デプステストに合格しなかったフラグメントは描画されない。
context.enable(DEPTH_TEST);また、必要であれば比較関数を変更することもできる。指定できる比較関数は、NEVER, ALWAYS, LESS, LEQUAL, EQUAL, GREATER, GEQUAL, NOTEQUALの8つ。デフォルトの比較関数はLESS(<)になっている。なお、デプステストは正規化デバイス座標で行われるので、奥の方が深度値は大きい。
context.depthFunc(LEQUAL); // 比較関数を≦に設定するステンシルテスト(Stencil Test)
ステンシルテストでは、 型抜きやマスクと呼ばれる機能が実現できる。あらかじめステンシルバッファというマスクデータ用のバッファを用意しておき、ステンシルバッファと比較することで、ピクセルを描画する・しないを決定する。画面の部分的な合成や、3Dモデルの縁取りなどに使われることが多い。
ステンシルテストについては、ここでは解説しない。
シザーテスト(Scissor Test)
シザーテストは描画可能領域を設定する。デフォルトではビューポートと同一の範囲になっている。画面の一部のみをクリアしたい場合などに使用するといいだろう。
context.enable(SCISSOR_TEST);
context.scissor(x, y, width, height); // 矩形領域を指定3D描画のプログラムを組む
大きな流れは2Dのときと変わらないので、前回の記事で説明した部分については省略する。前回と大差無い部分だけを先に書き出せば、だいたい以下のような形になる。ここに加えていこう。
import 'dart:html';
import 'dart:math';
import 'dart:async';
import 'dart:web_gl';
import 'dart:typed_data';
Future<List<String>> loadShaders() {
var loadVertexShader = HttpRequest.getString("vertex_shader.glsl");
var loadFragmentShader = HttpRequest.getString("fragment_shader.glsl");
return Future.wait([loadVertexShader, loadFragmentShader]);
}
void main() {
// シェーダを読み込んでから開始する。
loadShaders().then((shaders)=>start(shaders[0], shaders[1]));
}
void start(String vertexShaderSource, String fragmentShaderSource) {
// 表示用キャンバスの用意。
const WIDTH = 512;
const HEIGHT = 512;
var display = new CanvasElement(width:WIDTH, height:HEIGHT);
document.body.append(display);
// WebGL描画コンテキスト。
var context = display.getContext3d();
context.viewport(0, 0, display.width, display.height);
/*
* シェーダの準備。
*/
var vertexShader = context.createShader(VERTEX_SHADER);
context.shaderSource(vertexShader, vertexShaderSource);
context.compileShader(vertexShader);
var fragmentShader = context.createShader(FRAGMENT_SHADER);
context.shaderSource(fragmentShader, fragmentShaderSource);
context.compileShader(fragmentShader);
if(!context.getShaderParameter(vertexShader, COMPILE_STATUS)) {
var msg = context.getShaderInfoLog(vertexShader);
throw new Exception("Failed to compile vertex shader: $msg");
}
if(!context.getShaderParameter(fragmentShader, COMPILE_STATUS)) {
var msg = context.getShaderInfoLog(fragmentShader);
throw new Exception("Failed to compile fragment shader: $msg");
}
var program = context.createProgram();
context.attachShader(program, vertexShader);
context.attachShader(program, fragmentShader);
context.linkProgram(program);
if(!context.getProgramParameter(program, LINK_STATUS)) {
var msg = context.getProgramInfoLog(program);
throw new Exception("Failed to link program: $msg");
}
context.useProgram(program);
/*
* デプステストなどを有効にする。
*/
/*
* uniform変数を設定する。
*/
/*
* バッファの設定。
*/
var vertexBuffer = context.createBuffer();
var indexBuffer = context.createBuffer();
const POSITION_SIZE = 3;
const COLOR_SIZE = 3;
const STRIDE = Float32List.BYTES_PER_ELEMENT * (POSITION_SIZE + COLOR_SIZE);
const POSITION_OFFSET = 0;
const COLOR_OFFSET = Float32List.BYTES_PER_ELEMENT * POSITION_SIZE;
context.bindBuffer(ARRAY_BUFFER, vertexBuffer);
var positionLocation = context.getAttribLocation(program, "vertexPosition");
var colorLocation = context.getAttribLocation(program, "color");
context.enableVertexAttribArray(positionLocation);
context.enableVertexAttribArray(colorLocation);
context.vertexAttribPointer(positionLocation, POSITION_SIZE, FLOAT, false, STRIDE, POSITION_OFFSET);
context.vertexAttribPointer(colorLocation, COLOR_SIZE, FLOAT, false, STRIDE, COLOR_OFFSET);
/*
* 描画データ。
*/
var vertices;
var indices;
/*
* 描画する。
*/
context.bindBuffer(ARRAY_BUFFER, vertexBuffer);
context.bufferDataTyped(ARRAY_BUFFER, vertices, STATIC_DRAW);
context.bindBuffer(ELEMENT_ARRAY_BUFFER, indexBuffer);
context.bufferDataTyped(ELEMENT_ARRAY_BUFFER, indices, STATIC_DRAW);
context.drawElements(TRIANGLES, indices.length, UNSIGNED_SHORT, 0);
}行列計算用ライブラリ
Dartは標準では行列計算をサポートしていない。行列計算を楽にするために、pubspec.yamlのdependenciesにvector_mathライブラリを加えて、pub getを実行した後にimportしておこう。
import 'package:vector_math/vector_math.dart';ちなみにこのライブラリには変換行列を生成する機能がある。なので、この記事の大半を割いて説明した数学的な知識は一切不要ということになる。当初は標準ライブラリのみで説明する予定だったが、試しに書いてみたところ、あまりにも冗長になりすぎたため、ライブラリを使用することにした。あくまでWebGLの記事であって線形代数の記事ではないので、これでも十分だろう。
シェーダを書き換える
前回の記事ではシェーダをハードコーディングしていたが、外部ファイルに保存しておいた方がいいだろう。拡張子は特に決まりはないようで、glsl、shader、vert、fragなど各々好き勝手につけているようだ。ここでは.glslを使うことにする。
今回の主な変更は、全てバーテックスシェーダ側だ。変換行列の数だけ変数を作ることになる。基本的にはmodel、view、matrixの3つさえあればよいが、人によっては3つをまとめてmvpMatrixなどとしたり、逆にもっと細かくわけることもある。このあたりは好きにすればいいだろう。
変換行列の値は全ての頂点で共通になる。よってattribute変数で頂点ごとの値を設定する必要はない。こういうときはuniform変数を使用する。
attribute vec3 vertexPosition;
attribute vec3 color;
uniform mat4 model;
uniform mat4 view;
uniform mat4 projection;
varying vec4 vColor;
void main() {
// どうせアルファ値は1.0しか使わないのでrgbだけ送ってもらい
// ここで1.0を付け足す。
vColor = vec4(color, 1.0);
// そのまま、model→view→projectionの順でよい。
gl_Position = projection * view * model * vec4(vertexPosition, 1.0);
}フラグメントシェーダは単に色を書き込むだけでよい。
precision mediump float;
varying vec4 vColor;
void main() {
gl_FragColor = vColor;
}設定の変更
デプステストと背面カリングは有効にしておこう。この2つを使わないという場面は、そうそう無いと思われる。設定の変更はプログラム作成直後でいいだろう。
/*
* デプステストなどを有効にする。
*/
context.enable(DEPTH_TEST); // デプステスト
context.enable(CULL_FACE); // 背面カリングuniform変数の設定方法
uniform変数は頂点に依存しない変数だ。例えば、変換行列などは全ての頂点で共通のため、uniform変数として宣言されることが多い。位置を取得してから値を書き込むという流れはattribute変数と変わらないが、使用するメソッドが異なる。
/*
* uniform変数を設定する。
*/
UniformLocation projectionLocation = context.getUniformLocation(program, "projection"); // 変数の位置を取得する
context.uniformMatrix4fv(projectionLocation, false, projection); // 値を設定する面倒なのが値の設定方法で、シェーダ側の型によってメソッドが異なる。uniformMatrix4fvはmat4にfloatの配列を設定するメソッドになる。他にも、例えばuniform3fvはvec3へfloatの配列を設定するメソッドになるし、vのつかないuniform3f(location, false, x, y, z)はvec3の値を個別に指定できる。int型を使用するときはfのかわりにiを使い、uniform2ivというようなメソッドを使う。つまり、uniform + (Matrix) + 1|2|3|4 + f|i + vのような命名規則になっている。ただし、uniformMatrixにv無しのメソッドは存在しない。
変換行列に設定する値は後述する。
描画データの用意
今回も普通の四角形を用意する。後から様々な変換をほどこすので、初めから正規化デバイス座標に収める必要はない。単位(メートル、センチメートルなど)も好きなように決めてしまえばいい。また、背面カリングを有効化しているので、ワインディングオーダーが反時計回りであることには注意したい。
/*
* 描画データ。
*/
var vertices = new Float32List.fromList(<double>[-30.0, 30.0, 0.0, // 座標
0.0, 1.0, 0.0, // 色
-30.0, -30.0, 0.0,
1.0, 0.0, 0.0,
30.0, 30.0, 0.0,
1.0, 0.0, 0.0,
30.0, -30.0, 0.0,
0.0, 0.0, 1.0,]);
var indices = new Uint16List.fromList(<int>[0, 1, 2, 1, 3, 2]);変換行列の用意
準備が全て整ったので、改めて変換行列を用意していこう 。用意する行列は、モデル変換行列・ビュー変換行列・プロジェクション変換行列の3つだ。描画したいものにあわせて任意に設定するといいだろう。
/*
* uniform変数を設定する。
*/
// Model変換行列
// 拡大縮小・回転・平行移動を好きに組み合わせればよい。
// 拡大縮小と回転は原点中心に行われるので、
// 通常は平行移動より先に行う。
var rotation = new Matrix4.rotationZ(PI/8);
var translation = new Matrix4.translationValues(50.0, 0.0, -20.0);
var model = translation * rotation;
// View変換行列
// カメラ位置・見ている座標・上方向の3つで定義する。
// 上方向のベクトルは大雑把でかまわないが、
// カメラと水平になることだけは避けよう。
var cameraPosition = new Vector3(0.0, 60.0, 90.0);
var lookAtPosition = new Vector3.zero();
var upDirection = new Vector3(0.0, 1.0, 0.0);
var view = makeViewMatrix(cameraPosition, lookAtPosition, upDirection);
// Projection行列
// 今回は透視投影を使用する。
// なお、垂直視野角とアスペクト比から透視投影行列を作成する
// makePerspectiveMatrixというメソッドもある。普通はそちらを使用する。
var left = -40.0;
var right = 40.0;
var top = 40.0;
var bottom = -40.0;
var near = 30.0; // nearとfarは「Z座標」ではなく「距離」を表す。
var far = 150.0; // つまり、0 < near < far を満たす値を設定する。
var projection = makeFrustumMatrix(left, right, bottom, top, near, far);
// uniform変数を設定する。
// 位置を取得→値を設定の流れになる。
UniformLocation modelLocation = context.getUniformLocation(program, "model");
UniformLocation viewLocation = context.getUniformLocation(program, "view");
UniformLocation projectionLocation = context.getUniformLocation(program, "projection");
context.uniformMatrix4fv(modelLocation, false, model.storage);
context.uniformMatrix4fv(viewLocation, false, view.storage);
context.uniformMatrix4fv(projectionLocation, false, projection.storage);実行結果
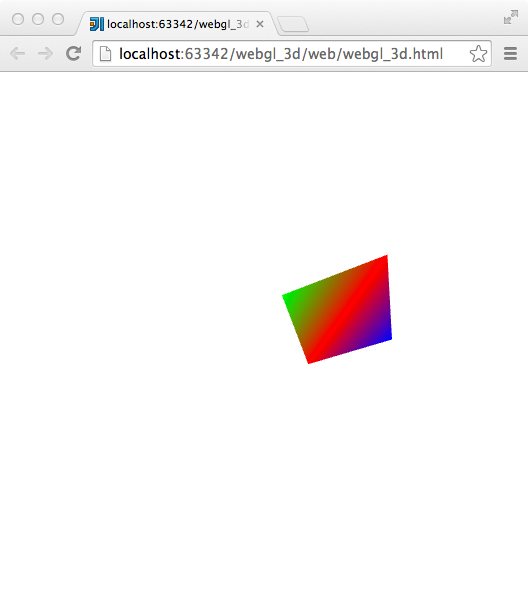
プログラムの実行結果
プログラムを実行すれば、カメラなどの設定に応じた描画がされるはずだ。
コード全体
import 'dart:html';
import 'dart:math';
import 'dart:async';
import 'dart:web_gl';
import 'dart:typed_data';
import 'package:vector_math/vector_math.dart';
Future<List<String>> loadShaders() {
var loadVertexShader = HttpRequest.getString("vertex_shader.glsl");
var loadFragmentShader = HttpRequest.getString("fragment_shader.glsl");
return Future.wait([loadVertexShader, loadFragmentShader]);
}
void main() {
// シェーダを読み込んでから開始する。
loadShaders().then((shaders)=>start(shaders[0], shaders[1]));
}
void start(String vertexShaderSource, String fragmentShaderSource) {
// 表示用キャンバスの用意。
const WIDTH = 512;
const HEIGHT = 512;
var display = new CanvasElement(width:WIDTH, height:HEIGHT);
document.body.append(display);
// WebGL描画コンテキスト。
var context = display.getContext3d();
/*
* シェーダの準備。
*/
var vertexShader = context.createShader(VERTEX_SHADER);
context.shaderSource(vertexShader, vertexShaderSource);
context.compileShader(vertexShader);
var fragmentShader = context.createShader(FRAGMENT_SHADER);
context.shaderSource(fragmentShader, fragmentShaderSource);
context.compileShader(fragmentShader);
if(!context.getShaderParameter(vertexShader, COMPILE_STATUS)) {
var msg = context.getShaderInfoLog(vertexShader);
throw new Exception("Failed to compile vertex shader: $msg");
}
if(!context.getShaderParameter(fragmentShader, COMPILE_STATUS)) {
var msg = context.getShaderInfoLog(fragmentShader);
throw new Exception("Failed to compile fragment shader: $msg");
}
var program = context.createProgram();
context.attachShader(program, vertexShader);
context.attachShader(program, fragmentShader);
context.linkProgram(program);
if(!context.getProgramParameter(program, LINK_STATUS)) {
var msg = context.getProgramInfoLog(program);
throw new Exception("Failed to link program: $msg");
}
context.useProgram(program);
/*
* デプステストなどを有効にする。
*/
context.enable(DEPTH_TEST); // デプステスト
context.enable(CULL_FACE); // 背面カリング
/*
* uniform変数を設定する。
*/
// Model変換行列
// 拡大縮小・回転・平行移動を好きに組み合わせればよい。
// 拡大縮小と回転は原点中心に行われるので、
// 通常は平行移動より先に行う。
var rotation = new Matrix4.rotationZ(PI/8);
var translation = new Matrix4.translationValues(50.0, 0.0, -20.0);
var model = translation * rotation;
// View変換行列
// カメラ位置・見ている座標・上方向の3つで定義する。
// 上方向のベクトルは大雑把でかまわないが、
// カメラと水平になることだけは避けよう。
var cameraPosition = new Vector3(0.0, 60.0, 90.0);
var lookAtPosition = new Vector3.zero();
var upDirection = new Vector3(0.0, 1.0, 0.0);
var view = makeViewMatrix(cameraPosition, lookAtPosition, upDirection);
// Projection行列
// 今回は透視投影を使用する。
// なお、垂直視野角とアスペクト比から透視投影行列を作成する
// makePerspectiveMatrixというメソッドもある。普通はそちらを使用する。
var left = -40.0;
var right = 40.0;
var top = 40.0;
var bottom = -40.0;
var near = 30.0; // nearとfarは「Z座標」ではなく「距離」を表す。
var far = 150.0; // つまり、0 < near < far を満たす値を設定する。
var projection = makeFrustumMatrix(left, right, bottom, top, near, far);
// uniform変数を設定する。
// 位置を取得→値を設定の流れになる。
UniformLocation modelLocation = context.getUniformLocation(program, "model");
UniformLocation viewLocation = context.getUniformLocation(program, "view");
UniformLocation projectionLocation = context.getUniformLocation(program, "projection");
context.uniformMatrix4fv(modelLocation, false, model.storage);
context.uniformMatrix4fv(viewLocation, false, view.storage);
context.uniformMatrix4fv(projectionLocation, false, projection.storage);
/*
* バッファの設定。
*/
var vertexBuffer = context.createBuffer();
var indexBuffer = context.createBuffer();
const POSITION_SIZE = 3;
const COLOR_SIZE = 3;
const STRIDE = Float32List.BYTES_PER_ELEMENT * (POSITION_SIZE + COLOR_SIZE);
const POSITION_OFFSET = 0;
const COLOR_OFFSET = Float32List.BYTES_PER_ELEMENT * POSITION_SIZE;
context.bindBuffer(ARRAY_BUFFER, vertexBuffer);
var positionLocation = context.getAttribLocation(program, "vertexPosition");
var colorLocation = context.getAttribLocation(program, "color");
context.enableVertexAttribArray(positionLocation);
context.enableVertexAttribArray(colorLocation);
context.vertexAttribPointer(positionLocation, POSITION_SIZE, FLOAT, false, STRIDE, POSITION_OFFSET);
context.vertexAttribPointer(colorLocation, COLOR_SIZE, FLOAT, false, STRIDE, COLOR_OFFSET);
/*
* 描画データ。
*/
var vertices = new Float32List.fromList(<double>[-30.0, 30.0, 0.0, // 座標
0.0, 1.0, 0.0, // 色
-30.0, -30.0, 0.0,
1.0, 0.0, 0.0,
30.0, 30.0, 0.0,
1.0, 0.0, 0.0,
30.0, -30.0, 0.0,
0.0, 0.0, 1.0,]);
var indices = new Uint16List.fromList(<int>[0, 1, 2, 1, 3, 2]);
/*
* 描画する。
*/
context.bindBuffer(ARRAY_BUFFER, vertexBuffer);
context.bufferDataTyped(ARRAY_BUFFER, vertices, STATIC_DRAW);
context.bindBuffer(ELEMENT_ARRAY_BUFFER, indexBuffer);
context.bufferDataTyped(ELEMENT_ARRAY_BUFFER, indices, STATIC_DRAW);
context.drawElements(TRIANGLES, indices.length, UNSIGNED_SHORT, 0);
}